skip to main |
skip to sidebar


Tengo 82 cm

Tengo 26 cm
Para que no olvide pensar "Pie se elevan al cuadrado"
(a pesar de que las empanadas suelen ser redondos)


lunes, 30 de mayo de 2016
Carrera Horas, minutos y segundos
http://www.primaria.librosvivos.net/archivosCMS/3/3/16/usuarios/103294/9/6EP_Mat_es_ud11_SumarRestarTiempo/frame_prim.swf
miércoles, 25 de mayo de 2016
El área de un círculo
El área de un círculo
Calculadora
Introduzca el radio, diámetro, circunferencia o área de un círculo para encontrar los otros tres.
Los cálculos se hacen "en vivo":
Introduzca el radio, diámetro, circunferencia o área de un círculo para encontrar los otros tres.
Los cálculos se hacen "en vivo":

© 2016 v0,85 MathsIsFun.com
Cómo calcular el Área
| El área de un círculo es π ( Pi ) veces el radio al cuadrado : |
A = π × r 2
| |
O bien, cuando se conoce el diámetro:
|
A = ( π / 4) x D 2
| |
O bien, cuando se conoce la circunferencia:
|
A = C 2 /4 π
|
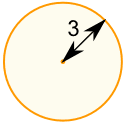
Ejemplo: ¿Cuál es el área de un círculo con un radio de 3 m?

Radio = r = 3
| Zona | = Π × r 2 | |
| = Π × 3 2 | ||
| = Π × (3 × 3) | ||
| = 3,14159 ... × 9 | ||
| = 28.27 m 2 (a 2 cifras decimales) |
La comparación de un círculo a una plaza
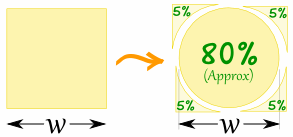
Es interesante comparar el área de un círculo con un cuadrado:

Un círculo tiene aproximadamente 80% de la área de un cuadrado similares de anchura.
El valor real es ( π / 4) = 0.785398 ... = 78.5398 ...%
El valor real es ( π / 4) = 0.785398 ... = 78.5398 ...%
¿Por qué? Debido a que la zona de la plaza es w 2
y el área del círculo es ( π / 4) x W 2
y el área del círculo es ( π / 4) x W 2
Ejemplo: Comparar un cuadrado a un círculo de 3 m de ancho
Área del cuadrado = w 2 = 3 2 = 9 m 2
Estimación del Círculo de Área = 80% de la zona de la plaza = 80% de los 9 = 7,2 m 2
Es cierto que la zona del círculo = ( pi / 4) x D 2 = ( pi / 4) x 3 2 = 7.07 m 2 (a 2 decimales)
La estimación de 7,2 m 2 no está lejos 7.07 m 2
Un ejemplo del "mundo real"
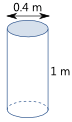
Ejemplo: Max está construyendo una casa. El primer paso consiste en perforar agujeros y llenarlos de hormigón.
Los agujeros son de 0,4 m de ancho y 1 m de profundidad , la cantidad de hormigón debe ordenar Max para cada hoyo?

Los agujeros son circular (en sección transversal ), ya que se perforan a cabo usando una barrena.
El diámetro es de 0,4 m, por lo que el área será:

A = ( π / 4) x D 2
A = (3.14159 ... / 4) x 0,4 2
A = 0.7854 ... × 0.16
A = 0.126 m 2 (a 3 decimales)
Y los agujeros son 1 m de profundidad, por lo que:
Volumen = 0.126 m 2 × 1 m = 0,126 m 3
Así que Max debe ordenar 0,126 metros cúbicos de concreto para llenar cada agujero.
Nota: Max podría haber estimado el área por:
- 1. Cálculo de un agujero cuadrado: 0,4 x 0,4 = 0.16 m 2
- 2. Tomar 80% de los que (las estimaciones de un círculo): 80% x 0.16 m 2 =0.128 m 2
- 3. Y el volumen de un agujero profundo 1 m es: 0,128 m 3
Pi ( π )
Pi ( π )
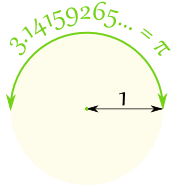 |
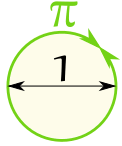
Dibujar un círculo con un radio de 1.
La forma en media distancia alrededor del círculo
es 3.14159265 ... un número conocido como Pi |
O podría dibujar un círculo con un diámetro de 1.
A continuación, la circunferencia (la distancia
todo el camino alrededor del círculo) será Pi | 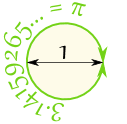 |
 |
Pi (el símbolo es la letra griega π ) es:
La relación de la circunferencia
al diámetro de un círculo. |

Para ayudarle a recordar simplemente dibujar este diagrama.
Hallazgo usted mismo Pi
Dibujar un círculo, o usar algo circular como un plato.
Mida alrededor del borde (la circunferencia ):

Tengo 82 cm
Medida a través del círculo (el diámetro ):

Tengo 26 cm
Dividir:
82 cm / 26 cm = 3,1538 ...
Esto se acerca bastante a π . Tal vez si medir con mayor precisión?
De hecho π es aproximadamente igual a:
3.14159265358979323846 ...
Los dígitos de seguir y seguir sin un patrón. Π se ha calculado que más de dos mil billones de decimales y todavía no hayningún patrón de los dígitos
|  |
Ejemplo: Se puede caminar alrededor de un círculo que tiene un diámetro de 100 metros, hasta dónde ha caminado?
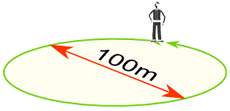 |
La distancia recorrida = Circunferencia = π × 100m m = 314,159 ...
= 314m (la más cercana m)
|
Aproximación
GEOMETRÍA: EL CÍRCULO
Circulo
 |
Un círculo es fácil de hacer:
Dibujar una curva que es "radio" de distancia
desde un punto central.
Y entonces:
Todos los puntos son la misma distancia del centro.
|
Puede dibujar usted mismo
Poner un alfiler en una tabla, poner un lazo de cuerda alrededor de ella, e insertar un lápiz en el bucle. Mantenga la cuerda estirada y dibujar el círculo!
|  |
Arrastre un punto!
© 2015 v0.86 MathsIsFun.com
Juega con ello
Pruebe a arrastrar el punto de ver cómo el radio y cirfcumference cambio.
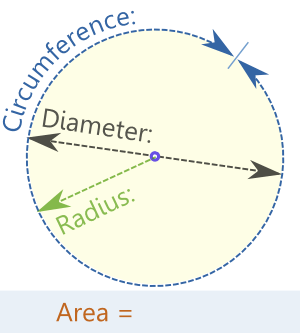
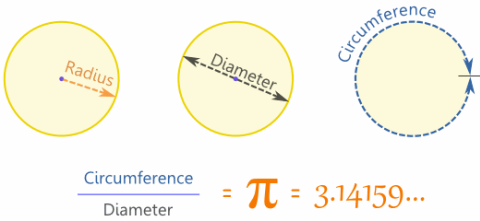
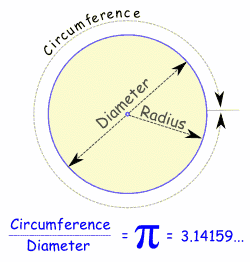
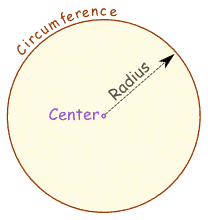
Radio, el diámetro y la circunferencia

La radio es la distancia desde el centro hacia fuera.
El diámetro se va directo a través del círculo, a través del centro.
La circunferencia es la distancia una vez alrededor del círculo.
Y aquí es lo mejor del libro:
Cuando dividimos la circunferencia por el diámetro obtenemos 3,141592654 ...
que es el número π ( Pi )
que es el número π ( Pi )
Así que cuando el diámetro es 1, la circunferencia es 3,141592654 ...
|  |
Podemos decir:
Circunferencia = π × Diámetro
Ejemplo: Se puede caminar alrededor de un círculo que tiene un diámetro de 100 metros, hasta dónde ha caminado?
 |
La distancia recorrida = Circunferencia = π × 100m
= 314m (la más cercana m)
|
También tenga en cuenta que el diámetro es dos veces el radio:
Diámetro = 2 × Radius
Y lo que también es cierto:
Circunferencia = 2 × π × Radius
Recordando
La longitud de las palabras puede ayudarle a recordar:
- Radius es la palabra más corta
- Diámetro es más largo (y es de 2 × Radio)
- Circunferencia es el más largo (y es π x diámetro)
Definición
El círculo es un plano de forma (en dos dimensiones):
Y la definición de un círculo es:
|  |
El conjunto de todos los puntos en un avión que sean una distancia fija de un centro.
Zona

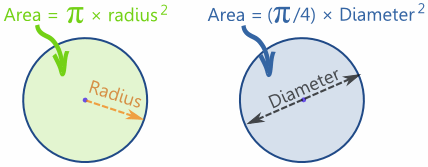
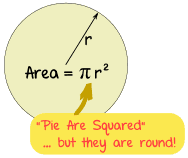
El área de un círculo es pi veces el radio al cuadrado, que está escrito:
A = π r 2

Para que no olvide pensar "Pie se elevan al cuadrado"
(a pesar de que las empanadas suelen ser redondos)
O bien, con el diámetro:
A = ( π / 4) x D 2
Ejemplo: ¿Cuál es el área de un círculo con un radio de 1,2 m?
A = π × r 2
A = π × 1,2 2
A = π x (1,2 x 1,2)
A = 3,14159 ... × 1,44 = 4,52 (a 2 decimales)
En comparación con el área de un cuadrado

Un círculo tiene aproximadamente 80% de la área de un cuadrado similares de anchura.
El valor real es ( π / 4) = 0,785398 ... = 78,5398 ...%
El valor real es ( π / 4) = 0,785398 ... = 78,5398 ...%
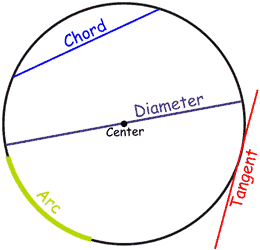
nombres
Porque la gente ha estudiado círculos desde hace miles de años los nombres especiales se han producido.
Nadie quiere decir "esa línea que comienza en un lado del círculo, pasa por el centro y termina en el otro lado" cuando una palabra como "Diámetro" va a hacer.
Así que aquí están los nombres especiales más comunes:

Líneas
Una línea que va de un punto a otro en la circunferencia del círculo se llama un acorde .
Si la línea pasa por el centro que se llama un diámetro .
Una línea que "apenas toque" el círculo que pasa por que se llama una tangente .
Y una parte de la circunferencia se llama un arco .
rebanadas
Hay dos principales "cortes" de un círculo.
La porción "pizza" se denomina Sector .
Y la rebanada hecha por un acorde se llama un segmento .
| 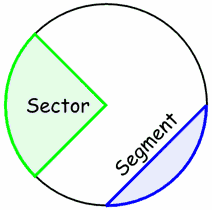 |
Sectores comunes
El cuadrante y semicírculo son dos tipos especiales de Sector:
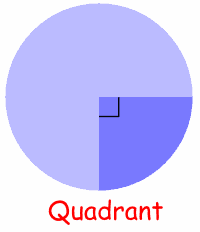 | Cuarto de círculo se denomina cuadrante . La mitad de un círculo se llama un semicírculo. |
 |
Dentro y fuera
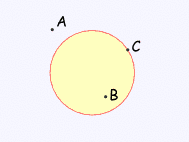 |
Un círculo tiene un interior y un exterior (por supuesto!). Pero también tiene un "sobre", ya que podríamos estar justo en el círculo.
Ejemplo: "A" es fuera del círculo, "B" se encuentra dentro del círculo y "C" está en el círculo.
|
lunes, 23 de mayo de 2016
APP DE PIZARRA DIGITAL
Para IPAD: Doceri
Para Tabletas Android:
Para Tabletas Android:
DownloadQR-Code
Características:
- Dibujo en tiempo real e intercambio de pizarra con una multitud de usuarios vía internet.
- Inicio de una sesión con un clic sin tener que crear una cuenta.
- Chat en vivo durante la sesión.
- Tableros ilimitados para dibujar.
- Posibilidad de guardar tus creaciones en tu galería o compartir a través de las redes sociales (Facebook, Twitter, Skype, Google +, Viber, etc.) o correo electrónico.
- Tamaños configurables para pincel y borrador, transparencia y color selector completo.
- Posibilidad de deshacer y rehacer un dibujo un número ilimitado de veces aún después de guardar los dibujos.
- Herramienta de texto para añadir notas y descripciones a las imagenes.
- Barra de herramientas ocultable que permite utilizar un tablero completo.
- Formas geométricas esenciales para completar cualquier dibujo.
- Dibujo en tiempo real e intercambio de pizarra con una multitud de usuarios vía internet.
- Inicio de una sesión con un clic sin tener que crear una cuenta.
- Chat en vivo durante la sesión.
- Tableros ilimitados para dibujar.
- Posibilidad de guardar tus creaciones en tu galería o compartir a través de las redes sociales (Facebook, Twitter, Skype, Google +, Viber, etc.) o correo electrónico.
- Tamaños configurables para pincel y borrador, transparencia y color selector completo.
- Posibilidad de deshacer y rehacer un dibujo un número ilimitado de veces aún después de guardar los dibujos.
- Herramienta de texto para añadir notas y descripciones a las imagenes.
- Barra de herramientas ocultable que permite utilizar un tablero completo.
- Formas geométricas esenciales para completar cualquier dibujo.
sábado, 14 de mayo de 2016
Entrada destacada
Repaso para control de CCNN La Materia
Es un power point muy largo. En él hay varios conceptos que no hemos trabajado, pero en sus primeras diapositivas está muy bien como repaso....

Blog Archive
DESCARGAS
Mi lista de blogs
La hora
Con la tecnología de Blogger.
Archives
-
►
2013
(31)
- ► septiembre (2)
-
►
2012
(50)
- ► septiembre (2)
-
►
2009
(14)
- ► septiembre (1)
-
►
2008
(107)
- ► septiembre (14)

















